Circular Measure (part 1)

Circular measure (part 1)

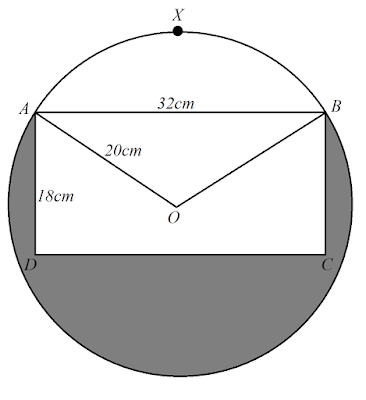
1. The diagram shows the circular cross-section of a uniform cylindrical log with centre $O$ and radius $20cm$. The points $A$, $X$ and $B$ lie on the circumference of the cross-section and $AB=32cm$

     i) Show that angle $AOB=1.855$ radians, correct to $3$ decimal places.

     ii) Find the area of the sector $AXBO$

     The section $AXBCD$, where $ABCD$ is a rectangle with $AD=18cm$, is removed

     iii) Find the area of the new cross-section (shown shaded in the diagram)

2. In the diagram, $OPQ$ is a sector of a circle, centre $O$ and radius $r$ cm. Angle $QOP=\theta$ radians. The tangent to the circle at $Q$ meets $OP$ extended at $R$.

     i) Show that the area, $Acm^{2}$, of the shaded region is given $A=\frac{1}{2}r^{2}(\tan \theta - \theta)$

     ii) In the case where $\theta=0.8$ and $r=15$, evaluate the length of the perimeter of the shaded region

3. The diagram shows a semicircle $ABC$ with centre $O$ and redius $8cm$. Angle $AOB=\theta$ radians

     i) In the case where $\theta=1$, calculate the area of the sector $BOC$

     ii) Find the value of $\theta$ for which the perimeter of sector $AOB$ is one half of the perimeter of sector $BOC$

     iii) In the case where $\theta = \frac{1}{3}\pi$, show that the exact length of the perimeter of triangle $ABC$ is $(24+8\sqrt{3})cm$

4. The diagram shows the sector $OPQ$ of a circle with centre $O$ and radius $rcm$. The angle $POQ$ is $\theta$ radians and the perimeter of the sector is $20cm$

     i) Show that $\theta=\frac{20}{r}-2$

     ii) Hence express the area of the sector in term of $r$

     iii) In the case where  $r=8$, find the length of the chord $PQ$.

5. In the diagram, $OCD$ is an isosceles triangle with $OC=OD=10cm$ and angle $COD=0.8$ radians. The points $A$ and $B$, on $OC$ and $OD$ respectively, are joined by an arc of a circle with centre $O$ and radius $6cm$. Find

     i) the area if the shaded region

     ii) the perimeter of the shaded region

6. In the diagram, $AC$ is an arc of a circle, centre $O$ and radius $6cm$. The line $BC$ is perpendicular to $OC$ and $OAB$ is straight line. Angle $AOC=\frac{1}{3}\pi$ radians. Find the area of the shaded region, giving your answer in term of $\pi$ and $\sqrt{3}$.

7. In the diagram, $ABC$ is semicircle, centre $O$ and radius $9cm$. The line $BD$ is perpendicular to the diameter $AC$ and angle $AOB=2.4$ radians.

     i) Show that $BD=6.08cm$, correct to $3$ significant figures.

     ii) Find the perimeter of the shaded region

     iii) Find the area of the shaded region

8. In the diagram, $OAB$ and $OCD$ are radii of a circle, centre $O$ and radius $16cm$. Angle $AOC=\alpha$ radians. $AC$ and $BD$ are arcs of circles, centre $O$ and radii $10cm$ and $16cm$ respectively.

     i) In the case where $\alpha=0.8$, find the area of the shaded region

     ii) Find the value of $\alpha$ for which the perimeter of the shaded region is $28.9cm$.